Vocabulaire
Domaine associé
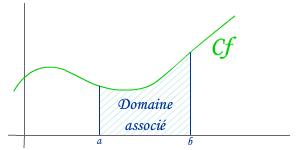
Nous appellerons E dommaine associé à une fonction f continue sur [a;b] le dommaine délimité par:
- Cf (la courbe représentative de f)
- L'axe des abscisses
- Les droites d'équation x=a et x=b
Unité d'aire
Le plan P muni d'un repere orthogonal (O;i;j) a pour unité d'aire u.a l'aire du rectangle bati a partir de O;I;J
I - Intégrale d'une fonction continue et positive
Définition:
soit f continue et positive sur [a;b]. L'intégrale de a à b de f est l'aire du domaine associé à f sur [a;b], exprimée en u.a. On la note:Cela se lit somme de a à b de f(x)dx, l'integrale est une somme infinie
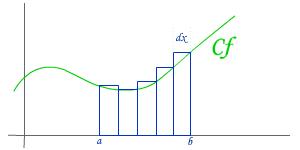
La théorie à d'abbord été posée par rieman, en prenant une somme d'aires simples (de rectangles) et en additionant toutes ces aires on peut obtenir un resultat d'autant plus proche de la réalité que la variation entre chaque base de battonet sera petite:
II - Intégrale d'une fonction continue
Définition:
Soit f une fonction continue sur [a;b] (a<b) Si f est négative alors:
Si f est de signe quelquonque, par exemple positive sur E1 et négative sur E2 alors:
III - Propriété
Théorème:
f et g continues sur un intervalle I contenant a,b et c. Pour tout a de I:
Pour a et b de I, tous reels alpha et beta:
Ces théorèmes sont admis (en réalité ils ne découlent pas de l'integrale mais la définissent, mais c'est cette approche que l'on garde en Terminale S)
Encadrement / Valeur moyenne
Théoreme:
f et g deux fonctions continues, pour a < b:
Théorème:
f fonction continue sur [a;b] (a<b)
La valeur moyenne de f entre a et b est:
De plus, il existe c
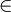[a;b] tel que:Preuve:
Supposons que f soit croissante.
Donc:
Et il existe c de [a;b] tel que (théoreme des valeurs intermediaires):
Pour une fonction qui n'est pas croissante, il faudrait établir que la continuité de f est le caractere fermé de [a;b] implique l'existence d'un minimum et d'un maximum atteint par f sur [a;b]
IV - Primitives
Définition
f est une fonction définie sur un intervalle I, une primitive de f est une fonction F dérivable sur I telle que :
Théorème
f une fonction définie sur I et admettant une primitive F sur I, alors:
- f admet une infinité de primitive
- Pour G, également primitive de f:
Preuve:
F dérivable sur I, G dérivable sur I:
G'(x)=F'(x)=f, donc (G-F)'=0, et par conséquent:
Corollaire:
x0 un réel donné de I, y0 un réel, il existe une unique primitive G de f tel que:
G(x0)=y0
Preuve:
Donc:
V - Intégrale et primitive
1) Définition/Théoreme
f continue sur un intervalle I, a
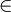IF définie sur I par:
Est l'unique primitive de f s'annulant en a.
Preuve:
Nous savons (cf théoreme précedent) qu'il existe ch
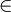[x0;x0+h] tel que:Donc:
Donc F Est bien une primitive de f, car:
Corollaire
f continue sur I, a et b deux reels de I et F une primitive de f, on note:
2) Intégration par partie
L'intégration par partie est en fait une méthode, il est un peu lourd d'apprendre par coeur ces fomules et d'autant plus simple de connaitre sur quoi elles sont basés: les opérations sur les dérivé!
Car: