Version imprimable
Préambule

Cette page n'a effectivement rien à voir avec mes cours. Il s'agit en fait d'une explication que j'avais envie d'écrire a propos d'un probleme algorithmique sur lequel j'ai travaillé et sur lequel il m'a semblé utile de mettre des lumières (Ca va interesser 5 personnes sur l'ensemble des visiteurs, mais peu importe :))
J'ai cherché moi même mais j'étais disons assez embêté alors j'ai finalement trouvé la réponse grâce à Internet  sous formes assez dures à assimiler, j'ai donc décidé de facilitr la vie à mes successeurs qui auraient envie de bien comprendre le raisonement assez peu intuitif de ce problème.

Cependant, il n'y a pas besoin de beaucoup de connaissance (surtout modulo) pour comprendre les explications que j'ai éssayé de rendre les plus simples possibles.


Le problème de Flavius Joséphus

"Josephus Flavius était un historien juif célèbre du premier siècle.
Pendant la guerre juive-romaine il a été pris au piège dans une caverne
avec un groupe de 40 soldats cernés par des Romains. La légende dît que,
préférant la mort à la capture, les Juifs décidèrent de former un cercle et
de tuer la troisième personne vivante rencontrée en suivant le parcours
autour du cercle; ceci jusqu'à ce qu'il ne reste qu'une personne :
cette personne devant se suicider. Josephus, pas très enthousiaste
à l'idée de mourir, trouva rapidement la bonne place dans le cercle
afin de rester en vie."

Histoire certes morbide mais on se contentera de considérer:


La base

L'idée de base est de rechercher bien entendu la position P ,et , pour des valeurs grandes de N et de K ça n'est pas si instinctif que ça !
Nous allons chercher à écrire un algorithme c'est à dire un ensemble d'opérations qui permettront de calculer quelque chose.

Pour ceux qui décrochent déja, vous pouvez regarder plus simplement ce qu'est un algorithme ici:


Par exemple (Inepte, je sais :)),  si on souhaite calculer UIndice de la suite pour une suite définie par:
On écrira le Pseudo-code ci-dessous:

U=3
Pour i de 1 à Indice de la suite:
    U=Ux2+4
Retourner U

Voila, un algorithme c'est juste ça, définir des variables et poser des boucles pour calculer quelque chose :) on peut aussi l'écrire sous la forme suivante (utile à la compréhension)

Fonction un(N)
    Si N=0: Retourner 3
    Autrement: Retourner 2*un(N-1)+4

Retourner un(Indice de la suite)


BIen, imaginons à présent le fonctionnement le plus simple (et aussi le plus lourd), je l'écris ci-dessous:

//On récupere les valeurs qui nous interessent
Demander N à l'utilisateur
Demander K à l'utilisateur
//On définit un tableau, qui contiendra:
// T[i]=1 si le personnage de rang i est encore dans le cercle
// T[i]=0 si le personnage e rang i n'y est plus
Définir un tableau T contenant N valeurs égales à 1
// On définit le nombre de personnes restantes, initialement N
// On définit I, le pointeur sur lequel on est, et S, la valeur
// de notre compte
Définir RESTANT=N
Définir I=0
Définir S=0
// On va "tourner" tant qu'il reste plus d'une personne
Tant que RESTANT est plus grand que 1
//Si le personnage est présent, on le compte (en faisant monter S)
//(autrement on ne compte rien du tout, evidement)
    Si T[i] est égal à 1
        Augmenter S
        // Si notre compte atteint K, on enleve le personnage (T[i]=0), on remet le
        // compteur s à 0 et on abaisse RESTANT de 1
        Si S est égal à K
            Définir T[i]=0
            Définir S=0
            Baisser RESTANT de 1
    // Enfin, on augmente le pointeur de 1, en prenant soin de revenir au début si
    // on est à la fin
    Augmenter I, si il est égal à N, I=0

// Finalement, la seule personne restante est la seule valeur P pour laquelle T[P]=1 !
Retourner le résultat P, (seule) valeur pour laquelle T[P]=1
   
Pfiiiiooooou ! Tout ça pour trouver P, assez fastidieux n'est-ce pas ?
Pourquoi ne pas s'arrêter là ? Parce qu'il y a nettement plus simple ! Et que l'algorithme ci dessus est une simulation gloutonne de la réalité qui, on va le voir, peut être vraiment simplifiée.


Récursivité (Non non ce n'est pas un truc de barbares) ?

Si je vous disait qu'on pouvait faire un algorithme qui aurait exactement les mêmes résultats que ci-dessus mais qui ne fait que quelques lignes ?! C'est possible ! Le tout part d'une idée, peu instinctive certes mais assez interessante qui est la suivante:

Notons solution(x)  la solution pour N=x et K donné (toujours constant dans notre expérience !)
Nous pouvons, facilement dire que:



Car si il n'y a qu'une seule personne, alors la seule possibilité, quelque soit k sera forcément la place 0 (On numérote de 0 à N-1 souvenez vous !), on peut aussi voir facilement que le premier elimine sera le Kieme prochain dans les N elements, c'est à dire (toujours en numérotant de 0 a N-1):




A quoi sert tout cela ? Vous allez comprendre un peu de patience, regardons donc un graphique, avec N=4 et K=2 par exemple



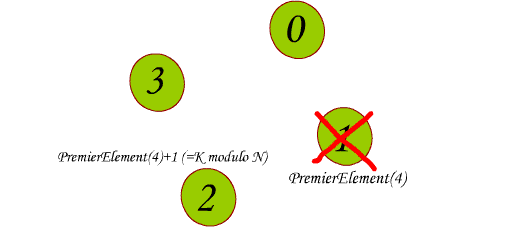
Nous avons éliminé un seul élément, c'est à dire compté 1, 2 et rayé le deuxième (Donc la boule 1)
Maintenant, partons de l'idée suivante: si on pouvait calculer la solution pour N=3, et K=2 a partir de l'élément 2, on aurait également notre solution ! Si on calcule donc solution(n-1) de maniere générale, et qu'on l'additionne au rang  du premier éliminé dans la boucle N, on aura le rang de la solution pour N !

Le rang obtenu Modulo N !

On a donc:


C'est à dire, en utilisant ce que l'on a écrit ci-dessus:


Bon, on respire ! On a presque fini notre démarche :)
En suivant la logique, on devra calculer Solution(n-1), qui nous renverra à son tour sur solution(n-2) et ainsi de suite. Au bout d'un moment, on trouvera fatalement une Solution(n-(n-1)) c'est à dire Solution(1), et ça on sait que c'est égal à 0 (voir ci-dessus) !

Bref, pour connaitre Solution(N) il suffit de connaitre:
Solution(N) < Solution(N-1) < ... < Solution(N-(N-1)) < Solution(1)

Allez, on va pas y passer la nuit !

Voici donc finalement le fameux algorithme:

//Pareil que tout à l'heure
Demander N à l'utilisateur
Demander K à l'utilisateur
// On écrit une fonction qui va s'apeller elle même
// jusqu'à ce qu'elle s'apelle avec N=1
Fonction solution(N)
    //Si N est égal a 1 on renvoi 0
    Si N est égal à 1
       Retourner 0
    //Autrement on renvoi ((K mod N)+solution(N-1)) mod N (comme vu ci-dessus!)
    Autrement
       Retourner ((K modulo N) + solution(N-1)) modulo N

// On apelle la fonction une seule fois (elle se rapelera elle même plein de fois
// par la suite !
Retourner solution(N)

Comme K est constant (seul N varie) on peut aussi dire que finalement, pour trouver Solution(N) on peut faire
Solution(1) > Solution(N-(N-1))  > ... > Solution(N-1) > Solution(N)
C'est à dire commencer par 1 puis réutiliser la variable obtenue, comme si on posait:
Et on écrit donc:

//Pareil que tout à l'heure
Demander N à l'utilisateur
Demander K à l'utilisateur
//On initialise P à 0 (solution(1))
Définir P=0
//On "balaye" notre "suite" jusqu'à atteindre N
Pour i de 2 à N: P=((K modulo i)+P) modulo i
// (Equivaut à): P=(K+P) modulo i

//On retourne la valeur de P
Retourner P

Conclusion

Voici une belle démonstration qui prouve (d'après moi qui ne suis qu'un élève de Terminale S, donc pas un pur scientifique ni philosophe evidement :)):

Voila, j'espere avoir interessé au moins une personne un jour avec cet article (je concois bien qu'il y a peut d'espoir :), personne qui lit ce message si cet article t'as plus envoi moi un mail ça me fera vraiment plaisir d'avoir aidé quelqu'un avec un truc comme ça :D)


Greg