I - Le noyau de l'atome
Un atome est constitué d'un noyau de diamètre de l'ordre de 10-15 m (1 fm - fentometre) et déelectrons formant le nuage électronique.

La probabilité de présence des éléctrons est d'autant plus proche qu'on est proche du noyau.
On note:
- L'élément chimique X
- Avec A nucléons (c'est à dire neutrons+protons)
- Avec Z Protons
Une force d'interaction environ 1000 fois plus puissante que l'interaction électrostatique maintient la cohésion de la matière (les charges possitives qui devraient se repousser). Les applications quantitatives de cette interaction sont trop complexes, on ne les traitera pas ici.
Généralement, la masse d'un atome est exprimée en unité de masse atomique noté u.
Il s'agit par définition du douzième de la masse d'un atome de carbone 12.
On en déduit donc:
- La masse d'un proton:
- La masse d'un neutron:
- La masse d'un éléctron:
Deux isotopes ont le même nombre de protons mais pas de neutrons.
On trouve sur Terre 90 élements stables qui correspondent en fait a 350 isotopes.
II - La radioactivité
A) Définitions
En 1896, Henri Becquerel découvre que certaines substances émettent spontanément des rayonements capables de traverser la matière.
Un échantillon radioactif peut émettre 3 types de particules et un rayonnement électromagnétique:
- Particules α, noyaux d'helium 4. Emises avec une vitesse de 20 000 Km/s, facilement arrêtées avec une feuille de papier
- Particule β: se déclinent en deux sous particules, à savoir:
- Les particules β-, des electrons. Emises a une vitesse de 280 000 km/s. arretés par une feuille d'aluminium
- Les particules β+, des positrons (ou antielectrons) emis a une vitesse de 280 000 km/s, facilement arrêtés (dès qu'ils rencontrent de la matière)
- Rayonement γ, onde électromagnetique de λ=10-4nm. Pour les arrêter il faut quelques mètres de béton.
Les noyaux stables gardent indéfiniment la même composition.
En revanche, les noyaux instables, entre autre radioactifs, se désintegrent (transforment) en émettant spontanément des particules α ou β souvent accompagnées d'un rayonement γ
Sur 350 noyaux naturels, environ 60 sont instables, ainsi que presque tous les noyaux artificels.
Le graphique representant le nombre de protons en fonction du nombre de neutrons est appellé carte N,Z, on y place:
- Les noyaux stables ("valée de la stabilité"):
Pour Z<20, les noyaux se situent au voisinage d'une droite Z=N
Pour Z>20, le nombre de neutrons augmente plus vite que le nombre de protons, les noyaux se situent en dessous de cette droite. - Les noyaux instables sont éparés en 3 cas:
- Excès de neutrons (en dessous de la vallée de la stabilité), se désintegrent par emission d'un électron: particules β-
- Défaut de neutrons (au dessus de la vallée de la stabilité) se désintegrent par émission d'un positon, ils sont radioactifs β+
Noyaux ayant un défaut de neutrons et dont A>170 se desintegrent par emission d'un noyau d'helium (radioactifs α)
B) Equations de désintegration nucléaire et lois de conservation.
Au cours d'une desintegration nucléaire, Z et A pour tous les noyaux et les particules mis en jeu sont conservés.
Radioactivité α
Radioactivité β-
Radioactivité β+
Les radioactivités β sont souvent accompagnées de particules de masse neglieable: les neutrinos. que l'on note:
Et 'anti neutrinos que l'on note:
Par soucis de simplification on ne les met pas dans les équations.
III - Evolution temporelle des systèmes radioactifs
Toute mesure de radioactivité (nombre de particules émises) est entachée d'un phénomene aléatoire (traitement statistique possible).
A) Pose des "bases"
Le raisonnement qui suit est assez simple en réalité et permet de bien comprendre de quoi on parle, rassurons nous en nous disant que tout tourne autout du même but (arriver à une équation différentielle)
On appellera ici n le nombre moyen de désintegrations durant une durée Δt
A la date t, l'échantillon radioactif comporte N noyaux non désintegrés.
A la date t+Δt, l'échantillon contient donc N-n noyaux non désintegrés.
La variation du nombre de noyaux radioactifs de l'échantillon se note:
Donc:
L'activité moyenne A(t) exprimée en becquerel (Bq) représente le nombre moyen de désintegrations que l'échantillon produit par seconde.
On montre également que l'activité A(t) est proportionelle au nombre de noyaux non désintegrés à la date t (c'est à dire à N(t))
Avec λ constante radioactive, qui dépend du noyau considéré et s'exprime en s-1.
Si on reprend donc les équations ci-dessus on peu écrire:
B) Loi de décroissance radioactive
Pour un petit intervalle de temps (durée infinitésimale)
Nous arrivons donc à une équation de type différentielle:
Une équation différentielle, si, comme moi à l'instant ou j'ai eu ce cours, vous n'en avez jamais parlé en maths, est une équation dans laquelle sont mis en jeu une fonction et sa dérivée.
L'équation différentielle ci dessus admet une solution de type exponentielle.
La loi de décroissance radioactive nous permet de la trouver.
En fait, l'équation de N(t) est:
Donc, si on dérive cette expression par rapport à t on obtient (en physique, la notation N' est dépréciée, on écrit donc dN/dt)
C'est à dire:
On retrouve donc notre équation différentielle.
C) Constante de temps et demi-vie
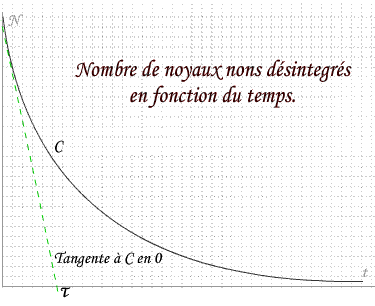
a) La constante de temps
Sur le graphique est représentée en vert la tangente à C en 0. Le point d'intersection entre la tangente et l'axe des abscisses est la constante de temps que l'on note:
Et que l'on exprime par conséquent en secondes.
AInsi:
b) la demie vie
La demie vie T est la durée au bout de laquelle la moitié des noyaux de l'échantillon se sont désintegrés.
Or:
La demi-vie T d'un isotope radioactif exprime la durée au bout de laquelle son activité est divisée par deux. Elle est reliée à la constante de temps par la relation:
Au bout d'une durée égale à 5~7 constantes de temps, 99% des noyaux se sont désintegrés
