Une lentille est une solide transparent limité par deux faces dont l'une est courbe ou spherique. Cela implique qu'il existe au moins un axe de symetrice qu'on apelle l'axe optique (Δ)
Une lentille est dite mince si l'épaisseur de sa partie centrale est negligeable devant sa hauteur. Sa partie centrale est alors appelée centre optique (O)


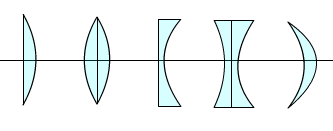
De gauche à droite: Plan convexe, Biconvexe, Plan concave, Biconcave, Menisque

Pour distinguer les lentilles on peut :

• Les toucher  (L'épaisseur des bords est plus grosse pour une lentille concave que convexe)
• En regardant un objet proche (Les lentilles convexes grossissent une image, comme une loupe )

Le symbole d'une lentille mince convexe est un segment sur l'axe optique (perpendiculaire et le coupant en O).


Le foyer principal image F' est le point de l'axe optique ou se rencontrent tous les rayons paralèlles à l'axe optique traversant la lentille.
Le foyer principal objet F est le symetrique de F' par rapport à O
La distance focale f, mesurée en m s'exprime par:


La vergence s'exprime en dioptrie (δ) et est donnée par:




On se restreint a l'étude des lentilles minces convergentes et on s'interesse à l'image d'un objet AB perpendiculaire et sur l'axe optique. L'image d'un point objet est le point de concours des rayons issus de cet objet après avoir traversé la lentille. On tracera donc le chemin des rayons remarquables issus du point objet.

Ces rayons remarquables sont les suivants:

• Un rayon paralèlle a ( Δ ) converge vers F'
• Un rayon passant par O n'est pas dévié
• Un rayon passant par F ressort paralèlle a ( Δ )

3) Grandissement et relation de conjugaison

Schéma de référence

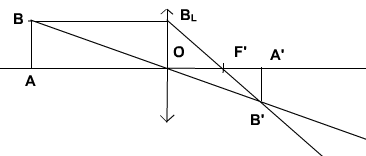
Ce schéma qui pourrait paraitre confus représente une lentille de centre optique O (coupée par l'axe optique). A gauche de la lentille l'objet AB et a droite son image A'B', remarquez qu'on a utilisé uniquement les rayons remarquables pour trouver B' et que A reste forcément sur l'axe optique.

a) Grandissement

Le grandissement est le rapport, en valeur algébrique de la taille de l'image A'B' et de la taille de l'objet AB

Ainsi on note la relation:



On peut également (grâce a une application de la configuration en papillon du théorème de Thalès) écrire:

b) Relation de conjugaison

Nous allons ici faire la démonstration de la relation de conjugaison, en utilisant encore Thalès, on remarque sur le schéma que:


Ainsi on peut dire:


Or, on peut décomposer la valeur algébrique:


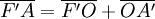
Ainsi on obtient:


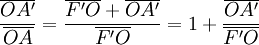
On divise les deux termes par la valeur algébrique de OA'  (la valeur algébrique de F'O est égal a -f ) :


Ainsi nous retrouvons notre relation de conjugaison:

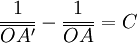
La formule (encadrée en rouge) ci-dessus est à connaître, cependant la démonstration n'est jamais demandée et il n'est pas la peine de la connaître par coeur

4) Conditions de Gauss

Nous avons considéré que l'image d'un point objet est un point. Dans ce cas la lentille est stigmatique et fournit une image nette
En réalité, le stigmatisme n'est qu'approché et d'autant mieux vérifié que les conditions de Gauss sont réspéctées, à savoir:

• Les rayons sont peu inclinés par rapport à l'axe optique (Objet petit et voisin de l'axe)
• Les rayons lumineux passent au voisinage du centre optique de la lentille (Diaphragme)

Loi de Descartes sur la réflexion:
Tout rayon lumineux incident frappant une surface réfléchissante avec un angle α par rapport à la normale est réfléchi dans le plan défini par le rayon incident et la normale, au delà de celle ci, et avec un angle β=α par rapport à la normale.
Cette phrase se traduit par le simple schéma :


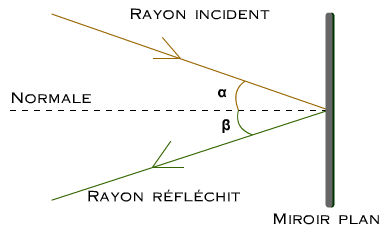
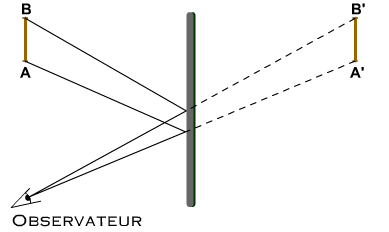
Conséquence: tout rayon lumineux issu d'un point objet A est vu par un observateur  au travers du miroir comme provenant du point image virtuel A', symetrique de A par rapport au plan du miroir.

Pour simplifier:
L'image d'un objet au travers d'un miroir est le symetrique de cet objet par rapport au plan du miroir.

2) Caracteristiques d'un miroir sphérique concave

a) Définition

La surface d'un tel miroir est délimitée par une sphere de rayon R (Rayon de courbure) et de centre C appelée aussi centre optique du miroir.
Vu en coupe, le miroir possède un axe de symetrie passant par C appelé axe optique du miroir.
L'axe optique du miroir rencontre le miroir en un point appelé le sommet (S)

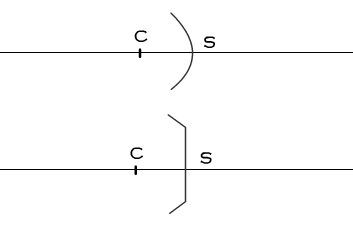
Au dessus, la représentation en coupe du miroir, en dessous, la représentation conventionnelle (qui évite de tracer un arc de cercle)

b) Foyer et distance focale

Pour des rayons lumineux passant au voisinage du sommet du miroir, on peut considérer qu'un faisceau de rayons paralèlles à l'axe optique du miroir converge en un point f de l'axe optique appelé foyer du miroir tel que :

Remarque: ceci est vrai dans les conditions de Gauss, où le miroir est dit stigmatique (les rayons sont peu inclinés par rapport à l'axe optique et passent au voisinage du sommet du miroir)

c) Conclusion

Grace a la loi de Descartes, on voit que:

• Tout rayon qui va passer par C est renvoyé "Sur lui même"
• Tout rayon arrivant sur le sommet S est réfléchi symetriquement par rapport à l'axe optique
• Tout rayon arrivant paralèlle à l'axe optique passe par F (dans les conditions de Gauss)
• Tout rayon passant par F ressort paralèlle à l'axe optique (dans les conditions de Gauss)

Quelques constructions:

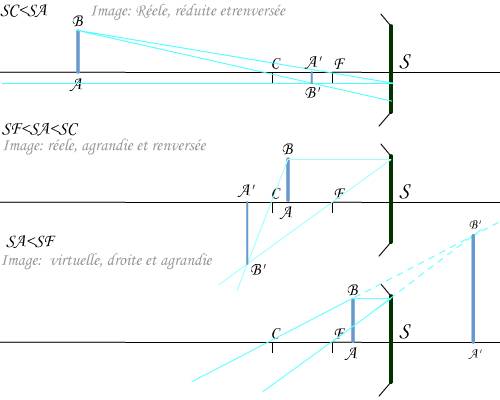
Dans le cas ou l'objet AB est supposé à l'infini l'image se forme dans le plan focale et on évalue la taille de l'objet (ou theta est l'angle d'observation):