Exponentielle, Logarithme népérien
Définitions et théoreme
Il existe une unique fonction f dérivable sur telle que:
telle que:
f'=f et f(0)=1
On la nomme exponentielle et on la note exp ou e.
Conséquences:
1) e0=1
2) e dérivable sur exp'(x)=exp(x)
exp'(x)=exp(x)
3) quelquesoit x dans , ex>0
, ex>0
4) exp est strictement croissante sur
Preuves:
- La définition implique les éléments 1) et 2)
- Pour prouver le 3) on raisonne par l'absurde:
Supposons qu'il existe a tel que ea<0, on a:
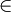 [ea;e0], d'après le théoreme des valeurs intermédiaires il existerait également un réel c dans [0;a] tel que:
[ea;e0], d'après le théoreme des valeurs intermédiaires il existerait également un réel c dans [0;a] tel que:
ec=0
Or exp ne s'annule pas, il est donc impossible que exp prenne des valeurs inférieures à 0
- Si partout exp'(x)=exp(x) et que exp est positive alors sa dérivée est elle aussi positive et exp est donc croissante ( 2) et 3) implique 4)
Notation:
1On établira plus tard que:
^n%20=%20e)

(La première égalité sera peut être établie plus tard en annexe)
Des lors:



Ainsi


ena=(ea)n se démontre par simple récurrence
^n=e^{n%20*%20\frac{a}{n}}%20=%20e^a)
Donc:




Preuve:

=e^x-x)
Est dérivable en tant que somme de fonctions dérivables.
=e^x-1=e^x-e^0)
0 est donc le minimum de φ
>0%20=>%20e^x%20\ge%20x) Et on sait que:
Et on sait que:

Alors

Et

On a:

^2)


Ainsi

On peut etendre la démonstration à:


 Nous n'étudierons pas encore ici pleinement la fonction logarithme mais seulement quelques explications la concernant (utiles notament en Physique)
Nous n'étudierons pas encore ici pleinement la fonction logarithme mais seulement quelques explications la concernant (utiles notament en Physique)
f est une bijonction de E dans F si f est une application telle que tout élément de F a un unique antécédant par f.
On note f-1 l'application de F dans E qui a un élément de f associe son antécedant par f.
On nomme f-1 la bijection réciproque de f (ou application réciproque).
Or nous savons que:
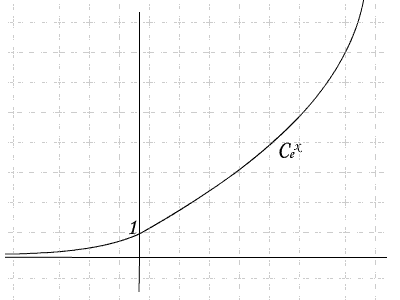
Exponentielle est strictement croissante et continue de dans ]0;+
dans ]0;+ [
[
Tout élement de ]0;+ [ a un unique antécedant dans
[ a un unique antécedant dans 
Donc ex est une bijection de dans ]0;+
dans ]0;+ [
[
Définition:
La fonction logarithme neperien est la bijection reciproque de la fonction exponentielle. On la note Ln

Ainsi:
(x)=x)
=x)
(y)=y)

\\%20y%20\in%20]0;+\infty[%20\end{matrix}%20\right)

Pour tous réels a et b strictement positifs et tout entier relatif n on a:







La fonction logarithme népérien est croissante, on peut prouver cela en raisonnant par l'absurde:
Si a est plus petit que b et que ln n'est pas croissante sur , alors on pourrait écrire:
, alors on pourrait écrire:

Or on pourrait dire que:

Car exponentielle est une fonction croissante sur , ce qui revient à dire:
, ce qui revient à dire:

Qui est en contradiction avec a plus petit que b, la fonction LN est donc croissante.
On a par conséquent: ln(2)>ln(1), donc ln(2)>0
Or:

D'où:

Donc

Pour la limite en moins l'infini, on peut utiliser la démonstration suivante:

Si y=ln(x) alors ey=x, on peut donc écrire:


La fonction ln est dérivable sur ]0;+ [ et:
[ et:
'(x)=\frac{1}{x})
Soit une fonction dérivable sur son ensemble de définition et à valeurs dans * alors (ln o u) est dérivable et:
* alors (ln o u) est dérivable et:
'=\frac{u'}{u})
ln est continue en 1:

Et la fonction exponentielle est continue en 1, or:


Lorsque alpha tend vers 0 x tend vers 1 et donc ln(x) tend vers 0
I - La fonction exponentielle
1) Généralité
Définitions et théoreme
Il existe une unique fonction f dérivable sur
 telle que:
telle que:f'=f et f(0)=1
On la nomme exponentielle et on la note exp ou e.
Conséquences:
1) e0=1
2) e dérivable sur
 exp'(x)=exp(x)
exp'(x)=exp(x)3) quelquesoit x dans
 , ex>0
, ex>04) exp est strictement croissante sur

Preuves:
- La définition implique les éléments 1) et 2)
- Pour prouver le 3) on raisonne par l'absurde:
Supposons qu'il existe a tel que ea<0, on a:
- exp est dérivable donc continue
- ea<0
- e0>0
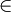 [ea;e0], d'après le théoreme des valeurs intermédiaires il existerait également un réel c dans [0;a] tel que:
[ea;e0], d'après le théoreme des valeurs intermédiaires il existerait également un réel c dans [0;a] tel que:ec=0
Or exp ne s'annule pas, il est donc impossible que exp prenne des valeurs inférieures à 0
Notes/Impressions:
Je donnerai peut être la démonstration qui explique pourquoi elle nécessite une certaine approche donc elle sera annéxée.
Je donnerai peut être la démonstration qui explique pourquoi elle nécessite une certaine approche donc elle sera annéxée.
- Si partout exp'(x)=exp(x) et que exp est positive alors sa dérivée est elle aussi positive et exp est donc croissante ( 2) et 3) implique 4)
Notation:
1On établira plus tard que:
2) Propriétés
- ea+b=ea*eb
-
-
- ena=(ea)n avec n
 Z
Z -
(La première égalité sera peut être établie plus tard en annexe)
Des lors:
Ainsi
ena=(ea)n se démontre par simple récurrence
Donc:
3) Propriété asymptotique
Preuve:
Est dérivable en tant que somme de fonctions dérivables.

0 est donc le minimum de φ
Alors
Et
On a:
Ainsi
On peut etendre la démonstration à:
4) Tableau des variations

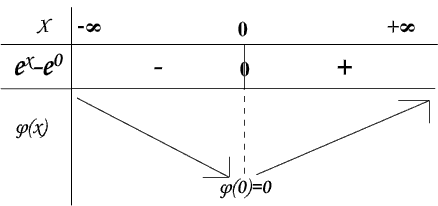
5) Courbe représentative

II - La fonction logarithme néperien
 Nous n'étudierons pas encore ici pleinement la fonction logarithme mais seulement quelques explications la concernant (utiles notament en Physique)
Nous n'étudierons pas encore ici pleinement la fonction logarithme mais seulement quelques explications la concernant (utiles notament en Physique)A) Définitions
f est une bijonction de E dans F si f est une application telle que tout élément de F a un unique antécédant par f.
On note f-1 l'application de F dans E qui a un élément de f associe son antécedant par f.
On nomme f-1 la bijection réciproque de f (ou application réciproque).
Or nous savons que:
Exponentielle est strictement croissante et continue de
 dans ]0;+
dans ]0;+ [
[
Tout élement de ]0;+
 [ a un unique antécedant dans
[ a un unique antécedant dans 
Donc ex est une bijection de
 dans ]0;+
dans ]0;+ [
[Définition:
La fonction logarithme neperien est la bijection reciproque de la fonction exponentielle. On la note Ln
B) Conséquences
Ainsi:
C) Ensemble de définitions et valeurs
D) Propriétés algébriques et limites
Théorème:
Pour tous réels a et b strictement positifs et tout entier relatif n on a:
Théorème:
Preuves:
La fonction logarithme népérien est croissante, on peut prouver cela en raisonnant par l'absurde:
Si a est plus petit que b et que ln n'est pas croissante sur
 , alors on pourrait écrire:
, alors on pourrait écrire:Or on pourrait dire que:
Car exponentielle est une fonction croissante sur
 , ce qui revient à dire:
, ce qui revient à dire:Qui est en contradiction avec a plus petit que b, la fonction LN est donc croissante.
On a par conséquent: ln(2)>ln(1), donc ln(2)>0
Or:
D'où:
Donc
Pour la limite en moins l'infini, on peut utiliser la démonstration suivante:
Si y=ln(x) alors ey=x, on peut donc écrire:
E) Dérivée, variation, signe
La fonction ln est dérivable sur ]0;+
 [ et:
[ et:Corollaire:
Soit une fonction dérivable sur son ensemble de définition et à valeurs dans
 * alors (ln o u) est dérivable et:
* alors (ln o u) est dérivable et:ln est continue en 1:
Et la fonction exponentielle est continue en 1, or:
Lorsque alpha tend vers 0 x tend vers 1 et donc ln(x) tend vers 0