I - La fonction exponentielle
1) Généralité
Définitions et théoreme
Il existe une unique fonction f dérivable sur
 telle que:
telle que:f'=f et f(0)=1
On la nomme exponentielle et on la note exp ou e.
Conséquences:
1) e0=1
2) e dérivable sur
 exp'(x)=exp(x)
exp'(x)=exp(x)3) quelquesoit x dans
 , ex>0
, ex>04) exp est strictement croissante sur

Preuves:
- La définition implique les éléments 1) et 2)
- Pour prouver le 3) on raisonne par l'absurde:
Supposons qu'il existe a tel que ea<0, on a:
- exp est dérivable donc continue
- ea<0
- e0>0
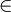 [ea;e0], d'après le théoreme des valeurs intermédiaires il existerait également un réel c dans [0;a] tel que:
[ea;e0], d'après le théoreme des valeurs intermédiaires il existerait également un réel c dans [0;a] tel que:ec=0
Or exp ne s'annule pas, il est donc impossible que exp prenne des valeurs inférieures à 0
Je donnerai peut être la démonstration qui explique pourquoi elle nécessite une certaine approche donc elle sera annéxée.
- Si partout exp'(x)=exp(x) et que exp est positive alors sa dérivée est elle aussi positive et exp est donc croissante ( 2) et 3) implique 4)
Notation:
1On établira plus tard que:
2) Propriétés
- ea+b=ea*eb
-
-
- ena=(ea)n avec n
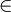 Z
Z -
(La première égalité sera peut être établie plus tard en annexe)
Des lors:
Ainsi
ena=(ea)n se démontre par simple récurrence
Donc:
3) Propriété asymptotique
Preuve:
Est dérivable en tant que somme de fonctions dérivables.
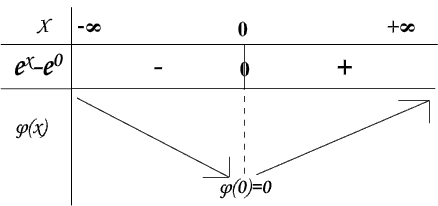
0 est donc le minimum de φ
Alors
Et
On a:
Ainsi
On peut etendre la démonstration à:
4) Tableau des variations
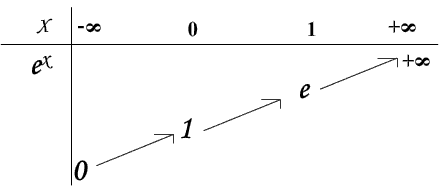
5) Courbe représentative
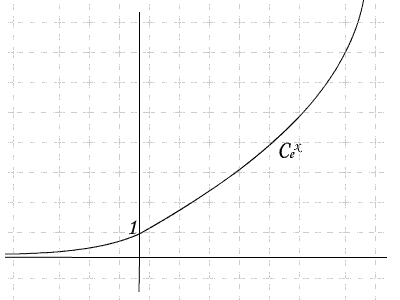
II - La fonction logarithme néperien
Nous n'étudierons pas encore ici pleinement la fonction logarithme mais seulement quelques explications la concernant (utiles notament en Physique)
A) Définitions
f est une bijonction de E dans F si f est une application telle que tout élément de F a un unique antécédant par f.
On note f-1 l'application de F dans E qui a un élément de f associe son antécedant par f.
On nomme f-1 la bijection réciproque de f (ou application réciproque).
Or nous savons que:
Exponentielle est strictement croissante et continue de
 dans ]0;+
dans ]0;+ [
[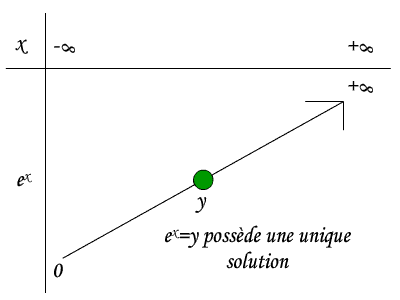
Tout élement de ]0;+
 [ a un unique antécedant dans
[ a un unique antécedant dans 
Donc ex est une bijection de
 dans ]0;+
dans ]0;+ [
[Définition:
La fonction logarithme neperien est la bijection reciproque de la fonction exponentielle. On la note Ln
B) Conséquences
Ainsi:
C) Ensemble de définitions et valeurs
D) Propriétés algébriques et limites
Théorème:
Pour tous réels a et b strictement positifs et tout entier relatif n on a:
Théorème:
Preuves:
La fonction logarithme népérien est croissante, on peut prouver cela en raisonnant par l'absurde:
Si a est plus petit que b et que ln n'est pas croissante sur
 , alors on pourrait écrire:
, alors on pourrait écrire:Or on pourrait dire que:
Car exponentielle est une fonction croissante sur
 , ce qui revient à dire:
, ce qui revient à dire:Qui est en contradiction avec a plus petit que b, la fonction LN est donc croissante.
On a par conséquent: ln(2)>ln(1), donc ln(2)>0
Or:
D'où:
Donc
Pour la limite en moins l'infini, on peut utiliser la démonstration suivante:
Si y=ln(x) alors ey=x, on peut donc écrire:
E) Dérivée, variation, signe
La fonction ln est dérivable sur ]0;+
 [ et:
[ et:Corollaire:
Soit une fonction dérivable sur son ensemble de définition et à valeurs dans
 * alors (ln o u) est dérivable et:
* alors (ln o u) est dérivable et:ln est continue en 1:
Et la fonction exponentielle est continue en 1, or:
Lorsque alpha tend vers 0 x tend vers 1 et donc ln(x) tend vers 0
